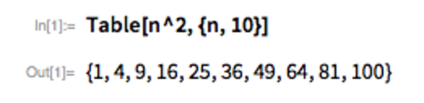(This post originally appeared on Stephen Wolfram's Blog)

But computational thinking is going to be needed everywhere. And doing it well is going to be a key to success in almost all future careers.
I’ve noticed an interesting trend. Pick any field X, from archeology to zoology. There either is now a “computational X” or there soon will be. And it’s widely viewed as the future of the field.
So how do we prepare the kids of today for this future? I myself have been involved with computational thinking for nearly 40 years now—building technology for it, applying it in lots of places, studying its basic science—and trying to understand its principles. And by this point I think I have a clear view of what it takes to do computational thinking. So now the question is how to educate kids about it. And I’m excited to say that I think I now have a good answer to that—that’s based on something I’ve spent 30 years building for other purposes: the Wolfram Language. There have been ways to teach the mechanics of low-level programming for a long time, but what’s new and important is that with all the knowledge and automation that we’ve built into the Wolfram Language we’re finally now to the point where we have the technology to be able to directly teach broad computational thinking, even to kids.
I’m personally very committed to the goal of teaching computational thinking—because I believe it’s so crucial to our future. And I’m trying to do everything I can with our technology to support the effort. We’ve had Wolfram|Alpha free on the web for years now. But now we’ve also launched ourWolfram Open Cloud—so that anyone anywhere can start learning computational thinking with the
Wolfram Programming Lab, using the Wolfram Language. But this is just the beginning—and as I’ll discuss here, there are many exciting new things that I think are now possible.
But how does one “tell a computer” anything? One has to have a language. And the great thing is that today with the Wolfram Language we’re in a position to communicate very directly with computers about things we think about.
The Wolfram Language is knowledge based: it knows about things in the world—like cities, or species, or songs, or photos we take—and it knows how to compute with them. And as soon as we have an idea that we can formulate computationally, the point is that the language lets us express it, and then—thanks to 30 years of technology development—lets us as automatically as possible actually execute the idea.
The Wolfram Language is a programming language. So when you write in it, you’re doing programming. But it’s a new kind of programming. It’s programming in which one’s as directly as possible expressing computational thinking—rather than just telling the computer step-by-step what low-level operations it should do. It’s programming where humans—including kids—provide the ideas, then it’s up to the computer and the Wolfram Language to handle the details of how they get executed.
Programming—and programming education—have traditionally been about telling a computer at a low level what to do. But thanks to all the technology we’ve built in the Wolfram Language, one doesn’t have to do that any more. One can express things at a much higher level—so one can concentrate on computational thinking, not mere programming.
Yes, there’s certainly a need for some number of software engineers in the world who can write low-level programs in languages like C++ or Java or JavaScript—and can handle the details of loops and declarations. But that number is tiny compared to the number of people who need to be able to think computationally.
The Wolfram Language—particularly in the form of Mathematica—has been widely used in technical research and development around the world for more than a quarter of a century, and endless important inventions and discoveries have been made with it. And all these years we’ve also been progressively filling out my original vision of having an integrated language in which every possibledomain of knowledge is built in and automated. And the exciting thing is that now we’ve actually done this across a vast range of areas—enough to support all kinds of computational thinking, for example across all the fields traditionally taught in schools.
Seven years ago we released Wolfram|Alpha—which kids (and many others) use all the time to answer questions. Wolfram|Alpha takes plain English input, and then uses sophisticated computation from the Wolfram Language to automatically generate pages of results. I think Wolfram|Alpha is a spectacular illustration—for kids and others—of what’s possible with knowledge-based computation in the Wolfram Language. But it’s only intended for quick “drive by” questions that can be expressed in fairly few words, or maybe a bit of notation.
So what about more complicated questions and other things? Plain English doesn’t work well for these. To get enough precision to be able to get definite results one would end up with something like very elaborate and incomprehensible legalese. But the good news is that there’s an alternative: the Wolfram Language—which is built specifically to make it easy to express complex things, yet is always precise and definite.
It doesn’t take any skill to use Wolfram|Alpha. But if one wants to go further in taking advantage of what computation makes possible, one has to learn more about how to formulate and structure what one wants. Or, in other words, one needs to learn to do computational thinking. And the great thing is that the Wolfram Language finally provides the language in which one can do that—because, through all the work we’ve put into it, it’s managed to transcend mere programming, and as directly as possible support computational thinking.
If it’s one kid, or a small group, I’ll always insist that the kids do the typing. Usually I’ll start off with something everyone knows. Get the computer to compute 2+2. They type it in, and they can see that, yes, the computer gives them the result they know:
They’ll often then try some other basic arithmetic. It’s very important that the Wolfram Language lets them just enter input, and immediately see output from it. There are no extra steps.
After they’ve done some basic arithmetic, I’ll usually suggest they try something that generates more digits:
Often they’ll ask if it’s OK, or if somehow the long number will break the computer. I encourage them to try other examples, and they’ll often do computations that instantly generate pages and pages of numbers. These kinds of big-number computations are something we’ve been able to do for decades, but kids still always seem to get very excited by them. I think the point is that it lets them see that, yes, a computer really can compute nontrivial things. (Just think how long it would take you to compute all those digits…)
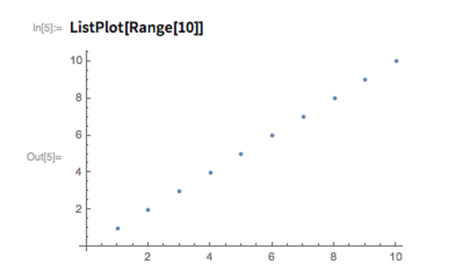
After they’ve done some basic arithmetic, it’s time for them to try some other functions. The most common function that I end up starting with is Range:
Range is good because it’s easy for kids to see what it does—and they quickly get the sense that, yes, they can tell the computer to do something, and it will do it. Range is also good because it’s easy to use it to generate something satisfyingly big. Often I’ll suggest they try Range[1000]. They’ll ask ifRange[10000] is OK too. I tell them to try it…
I think I do something different with every kid or group of kids I deal with. But a pretty common next step is to see how to visualize the list we’ve made:
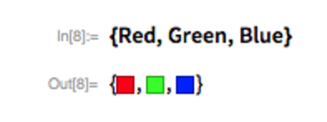
For kids who perhaps don’t think they like math—or tech in general—I might instead make some colors:
We might also get a bit more sophisticated with color:
Perhaps then we’d go in another direction, getting a list of common words in English (I’d also try another language if any of the kids know one):
Some kid might ask “what about the first two letters?”. Then we’d be off trying that (yes, there’s some computational thinking involved in that UpTo):
We might talk for a bit about how many words start with “un-” etc. And maybe we’d investigate some of those words. We could go on and look at translations of words:
Actually, it’d be easy to go on for hours just doing things with what I’ve talked about so far. But let’s look at some other examples. A big thing about the Wolfram Language is that it knows about lots of real-world data. I’d typically build this up through a bunch of steps, but here’s an example of making a collage of flags of countries in Europe, where the size of each flag is determined by the current population of the country:
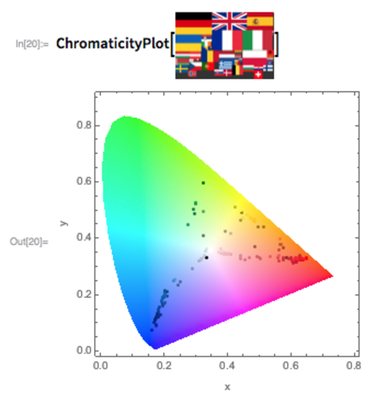
Since we happen to have talked about color, it’s fun to see where in color space the flags lie (apparently not many “pink countries”, for example):
A big theme is that the Wolfram Language lets one do not just abstract computation, but computation based on real-world knowledge. The Wolfram Language covers a huge range of areas, from traditional STEM-like areas to art, history, music, sports, literature, geography and so on. Kids often like doing things with maps.
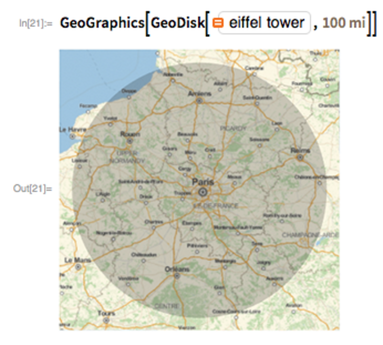
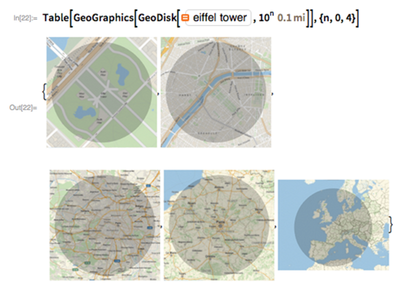
We might start from where we are (Here). Or from some landmark. Like here’s a map with a 100-mile-radius disk around the Eiffel tower:
Here’s a “powers of 10” sequence of images:
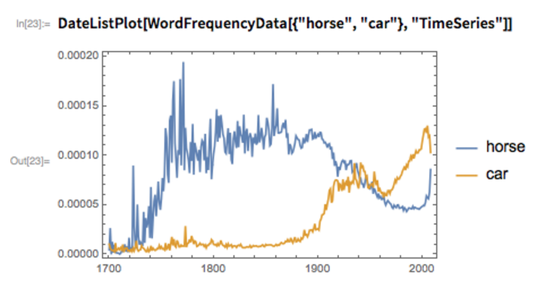
So what about history, for example? How can the Wolfram Language engage with that? Actually, it’s full of historical knowledge. About countries (plot the growth and decline of the Roman Empire), or movies (compare movie posters over time), or, for example, words. Like here’s a comparison of the use of “horse” and “car” in books over the last 300 years:
Try the same thing for names of countries, or inventions, or whatever; there’s always lots of history to discuss.
There are so many different directions to go. Here’s another one: graphics. Let’s make a 3D sphere:
It’s always fun for kids that they can make something like this in 3D and move it around. If they’re on the more sophisticated end, we might build up 3D graphics like this from 100 random spheres with random colors:
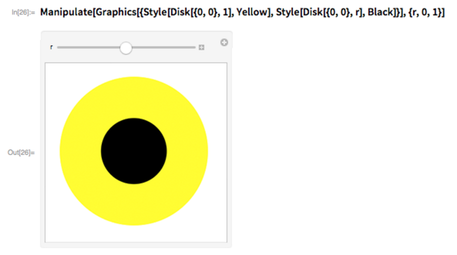
Kids of all ages like making interactive stuff. Here’s a simple “adjustable Cyclops eye” that one can easily build up to in stages:
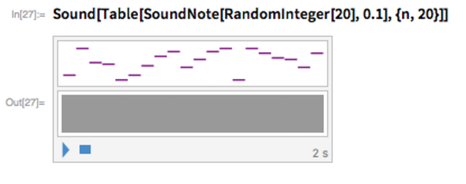
Another thing I sometimes do is have the Wolfram Language make sound. Here’s a random sequence of musical notes:
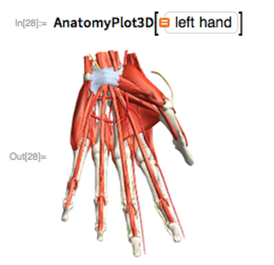
There are so many directions to go. For the budding medical person, there’s anatomy in 3D—and you can pick out the geometry of a bone and 3D print it. And so on and so on.
But What About...
The first was that they were skeptical that kids would actually be able to type raw code in the Wolfram Language; they thought they’d just get too confused and tangled up with syntax and so on. And the second issue is that they didn’t think kids would be motivated to do anything with code unless it led to creating a game they could play.
One of the nice features of working with kids is that if you give them the chance, they’ll very quickly make it very clear to you what works with them and what doesn’t. So what actually happens? Well, it turns out that in my experience neither of the potential problems people brought up ends up being a real issue at all. But the reasons for this are quite interesting, and not particularly what I would have expected.
About typing code, one thing to realize is that in today’s world, most middle-school-age kids are quite used to typing, or at least typing text. Sometimes when they start typing code they at first have to look where the [ ] keys are, or even where the + is. But they don’t have any fundamental problem with typing. They’re also quite used to learning precise rules for how things work (“i comes before e …” in English spelling; the order of operations in math; etc.). So learning a few rules like “functions use square brackets” or “function names start with capital letters” isn’t a big deal. And of course in the Wolfram Language there’s nothing like all those irregularities that exist in a natural language like English.
When I watch kids typing code, the automatic hints we provide are quite important (brackets being purple until they’re matched; things turning red if they’re in the wrong place; autocompletions being suggested for everything; etc.). But the bottom line is that despite the theoretical concerns of adults, actual kids seem to find it extremely easy to type syntactically correct code in the Wolfram Language. In fact, I’ve been amazed at how quickly many kids “get it”.
Having seen just a few examples, they immediately generalize. And the great thing is that because the Wolfram Language is designed in a very consistent way, the generalizations they come up with actually work. It’s heartwarming for me as the language designer to see this. Though of course, to the kids it’s just obvious that something must work this-or-that way, and they don’t imagine that it took effort to design it that way.
OK, so kids can type Wolfram Language code. But do they want to? Lots of kids like playing games on computers, and adults often think that’s all they’ll be interested in creating on computers too. But in my observation, this simply isn’t true. The most important thing for most kids about the Wolfram Language is that they can immediately “do something real” with it. They can type whatever code they want, and immediately get the computer to do something for them. They can create pictures or sounds or text. They can make art. They can do science. They can explore human languages. They can analyze Pokémon (yes, the Wolfram Language has extensive Pokémon data). And yes, if they really want to, they can make games.
In my experience, if you ask kids before they’ve seen the Wolfram Language what they might be interesting in programming they’ll often say games. But as soon as they’ve actually seen what’s possible in the Wolfram Language, they’ll stop talking about games, and they’ll want to do something “real” instead.
The first point is that the Wolfram Notebook concept that we invented nearly 30 years ago is a really good way for kids (and others) to interact with the language. The idea of a notebook is to have an interactive document that freely mixes code, results, graphics, text and everything else. One can build up a computation in a notebook, typing code and getting results right there in the document. The results can be dynamic—with their own automatically generated user interfaces. And one can read—or write—explanations or instructions directly in the notebook. It’s taken decades to polish all aspects of notebooks. But now we’ve got an extremely efficient and wonderful environment in which to work and think—and learn computational thinking.
For many years, notebooks and the Wolfram Language were basically available only as desktop software. But now—after a huge software engineering effort—they’re also available in the cloud, directly in a web browser, or on mobile devices. So that means that any kid can just go to a web browser, and immediately start interacting with the Wolfram Language—creating or editing a notebook, and writing whatever code they want.
It takes a big stack of technology to make this possible. And building it has taken a big chunk of my life. It’s been very satisfying to see so many great leading-edge achievements made over the years with our technology. And now I’m really excited to see what’s possible in using it to spread computational thinking to future generations.
I made the decision when we created Wolfram|Alpha to make it available free on the web to the world. And it’s been wonderful to see so many people—and especially kids—using it every day. So a few months ago, when the technology was ready, I made the decision also to provide free access to the whole Wolfram Language in our Wolfram Open Cloud—and to set it up so kids (and others) could learn computational thinking there.
Wolfram|Alpha is set up so anyone can ask it questions, in plain English. And it’s turned out to be great—among other things—as a way to support education in lots of fields. But if one wants to learn true computational thinking for the future, then one’s got to go beyond asking questions in plain English. And that’s where the Wolfram Language comes in.
So what’s the best way to get started with the Wolfram Language, and the computational thinking it makes possible? There are probably many answers to this, that, among other things, depend on the details of the environment and resources that different kids have available. I’d like to think I’ve personally done a decent job working directly with kids—and for example at our Wolfram Summer Camp for high-school students I’ve seen very good things achieved with direct personal mentoring.
But it’s also important to have “self service” solutions—and one thing I’ve done to contribute to that is to write a book called An Elementary Introduction to the Wolfram Language. It’s really a book about computational thinking. It doesn’t assume any previous knowledge of programming, or, for example, of math. But in the course of the book it gets people to the point where they can routinely write real programs that do things they’re interested in.
The book is available free online. And it’s also got exercises—which are automatically graded in the cloud. I originally intended the book for high school and up. But it’s turned out that there’s ended up being quite a collection of middle-school students (aged 11 and up) who have enthusiastically worked their way through it—even as the book has also turned out to be used for things like graduate math courses, trainings at banks, and educating professional software developers.
There’s a (free) online course based on my book that will be available soon, and I know there are quite a few courses under development that use the book to teach modern programming and computational thinking.
But, OK, when a kid walks up to their web browser to learn computational thinking and the Wolfram Language, where can they actually go? A few months ago we launched Wolfram Programming Labas an answer to this. There’s a version in the Wolfram Open Cloud that’s free (and doesn’t even require login so long as you don’t want to save your work).
Wolfram Programming Lab has two basic branches. The first is a collection of Explorations. Each Exploration is a notebook that’s set up to contain code you can edit and run to do something interesting. After you’ve gone through the code that’s already there, the notebook then suggests ways to go further, and to explore on your own.
Explorations let you get a taste of the Wolfram Language and computational thinking. Kids can typically get through the basics of several in an hour. In a sense they’re like “immersion language learning”: You start from code that “fluent speakers” might write, then you interact with it.
But Wolfram Programming Lab provides a second branch too: an interactive version of my book, that lets people go step-by-step, building up from a very simple start, and progressively creating more and more sophisticated code.
You can use Wolfram Programming Lab entirely through a web browser, in the cloud. But there’s also a desktop version that runs on any standard computer—and lets you get really zippy local interactivity, as well as letting you do bigger computations if you want. And if you have a Raspberry Pi computer, the desktop version of Wolfram Programming Lab comes bundled right with the operating system, including special features for getting data from sensors connected to the Raspberry Pi.
I’ve wanted to make sure that Wolfram Programming Lab is suitable for any kid, anywhere, whether or not they’re embedded in an educational environment that can support what they’re doing. And from what we can tell, this seems to be working nicely—though it certainly helps when kids have actual people they can work with. We plan to set up the structure for informal networks to support this, among other things using the existing, very active Wolfram Community. But we’re also setting things up so Wolfram Programming Lab can easily fit into existing, organized, educational settings—not least by using the Wolfram Language to create some of the world’s best educational analytics to analyze student progress.
It’s worth mentioning that one of the great things about our whole Wolfram Cloud infrastructure is that it lets anyone—whether they’re students or teachers—directly publish things on the web for the world to use. And in Wolfram Programming Lab, for example, it’s routine to end up deploying an app on the web as part of an Exploration.
We’re still in the early days of understanding all the nuances of actually deploying Wolfram Programming Lab in every possible learning environment—and we’re steadily advancing on many fronts. A little while ago I happened to be talking to some kids at a school in Korea, and asked them whether they thought they’d be able to learn the Wolfram Language. One of the kids responded that she thought it looked easy—except for having to read all the English in the names of the functions.
Well, that got me thinking. And the result was that we introduced multilingual code captions, that annotate code in a whole range of different languages. You still type Wolfram Language code using standard function names, but you get an instant explanation in your native language. (By the way, there are also versions of my book that will be available in various languages.)
One might think that computational thinking was somehow only relevant to STEM education. But it’s not true. Computational thinking is relevant across the whole curriculum. To social studies. To language arts. To music. To art. Even to sports. People have tried to make math relevant to all these areas. But you just can’t do enough with traditional hand-calculation-based math to make this realistic.
But with computation and computational thinking it’s a completely different story. In every one of these areas there are very powerful—and often very clarifying—things that can be done with computation and computational thinking. And the great thing is that it’s all accessible to kids. The Wolfram Language takes care of all the internal technicalities—so one can really focus on the pure computational thinking and understanding, without the mechanics getting in the way.
One way to get to this is to extend what one imagines “math” education to be—and that’s a large part of what Computer-Based Math is doing. But another approach is just to think about inserting computational thinking directly into every other area of the curriculum. I’ve noticed that in practice—particularly at the grade school level—the teachers who get enthusiastic about teaching computational thinking may or may not have obvious technical backgrounds. It’s like with the current generation of kids: you don’t have to be a techie to be into knowledge-based programming and computational thinking.
In the past, with low-level computer languages like C++ and Java, you really did have to be a committed, engineering-oriented person to be teaching with them. But it’s a completely different story with the Wolfram Language. Yes, there’s plenty to learn if one wants to know the language well. But one is learning about general computational thinking, not the engineering details of computer systems.
So how should computational thinking be fitted into the school curriculum? Something I hear quite a lot is that teachers already have a hard time fitting everything they’re supposed to teach into the available time. So how can anything else be added? Well, here’s the surprising thing that I’m only just beginning to understand: adding computational thinking actually makes it easier to teach lots of things, so even with the time spent on computational thinking, the total time can actually go down, even though there’s more being learned.
How can this be? The main point is that computational thinking provides a framework that makes things more transparent and easier to understand. When you formulate something computationally, everyone can try it out and explicitly see how it works. There’s nothing hidden that the student somehow has to infer from some comment the teacher made.
Here’s a story from years ago, when the Wolfram Language—in the form of Mathematica—was first being used to teach calculus. It’s pretty common for calculus students to have trouble understanding the concept of a function. But professors told me that they started noticing that when they were learning calculus through Mathematica, somehow none of the students ended up being confused about functions. And the reason was that they had learned about functions through computational thinking—through seeing them explicitly and computationally in the Wolfram Language, rather than hearing about them more indirectly and abstractly as in standard calculus teaching.
Particularly in past decades there was a great tendency for textbooks in almost every subject to “stand on ceremony” in explaining things—so the best explanations often had to be sought out in semi-illicit outline publications. But somehow, with things like MathWorld and Wikipedia, a more direct style of presenting information has become commonplace—and has come to be taken for granted by today’s students. I see the application of computational thinking across every field as being a kind of dramatic continuation of this trend: taking things which could only be talked around, and turning them into things that can be shown through computation directly and explicitly.
You talk about a Shakespeare play and try to get a general sense of the flow in it. Well, with computational thinking you can imagine creating a social network for the play (who “knows” who through being in the same scene, etc.). And pretty soon you have a nice summary, that’s a place to launch from in talking about the nuances of the play and its themes.
Imagine you’re talking about different language families. Well, you can just take some words and use WordTranslation to translate them into hundreds of languages. Then you could make adendrogram to show how the forms of those words cluster in different languages—and you can discover the Indo-European language family.
You could be talking about styles of art—and pull up lots of images of famous paintings that are built into the Wolfram Language. Then you could start comparing the use of color in different paintings—maybe making a plot of how it changed over time, seeing if one can tell when different styles came in.
You could be talking about the economics of different countries—and you could immediately create your own infographics, working with students to see how best to present what’s important. You could be talking about history, and you could use the historical map data in the Wolfram Language to compare the conquests of Alexander the Great and Julius Caesar. Or you could ask about US presidents, make a timeline showing their administrations, and compare them using economic or cultural indicators.
Let’s say you’re teaching English grammar. Well, it certainly helps that the Wolfram Language can automatically diagram sentences. But you can also let students try their own rules for generating sentences—so they can see what generates something they think is grammatically correct, and what doesn’t. How about spelling? Can computational thinking help with that? I’m not sure. It’s certainly easy to take all the common words in English, and start trying out different rules one might think of. And it’s fun to discover exceptions (does “u” always follow “q”: it’s trivial in the Wolfram Language to find out).
It’s an interesting exercise to take standard pieces of the curriculum for different subjects and ask “can this be helped by applying computational thinking?”. Sometimes the first thing one thinks of may be a gimmick. But what I’ve found is that if one really asks what the point of that piece of the curriculum is, there will end up being a way that computational thinking can help, right from the foundations.
Over time, there will be a larger and larger inventory of great examples of all this. In the past, with math (the non-computer-based version), it’s been rather disappointing: there just aren’t that many examples that work. Yes, there are things like exponential growth that show up in a bunch of places, but by the time one realizes that the examples in the calculus books are in many cases the same as they were in the 1700s, it’s not looking so good. And with standard programming the picture isn’t much better: there are only so many places that the Fibonacci sequence shows up. But with knowledge-based programming in the Wolfram Language the picture is completely different. Because the language immediately connects to the data and computations that are relevant across essentially every domain.
OK, so if one’s going to be teaching computational thinking, how should it be organized? Should one for example have a Computational Thinking class? At the college level, I think Computational Thinking 101 is a good idea. In fact, it might well be the single most important course many students take. At the high-school level, I think it’s less obvious what should be done, and though I’m certainly no expert, my tendency is to think that computational thinking is better inserted into lots of different modules within different classes.
One obvious question is: what’s the startup cost to having students engage with computational thinking? My feeling is that with the technology we’ve got now, it’s extremely low. With Wolfram|Alpha, it’s zero. With Explorations in the Wolfram Language, it’s very close to zero. With free-form code in the Wolfram Language, there’s a small amount to know, and perhaps it’s better for this to be taught in one go, a little like a miniature version of what would be a “service math course” at the college level.
It’s worth mentioning that computational thinking is rather unique in its breadth of applicability across the curriculum.
Everyone would like what’s learned in one class to be applied in others, but it doesn’t happen all that often. I’ve already mentioned the difficulties with traditional math. The situation is a bit better with writing, where one would at least hope that students use what they’ve learned in producing essays in other subjects. But most fields are taught in intellectual silos, with nothing learned in one even being referenced in others. With computational thinking, though, there’s vastly more cross-connection. The social network for the Shakespeare play involves the same computational ideas as a network for international trade, or a diagram of the relations between words in different languages. The visualization technique one might use for economic performance is the same as for sports results. And so on.
So what’s made this possible? It’s basically the layers and layers of automation that we’ve built into the Wolfram Language over the past thirty years. The goal is to automate as much as possible—so that the humans who use the Wolfram Language, whether they’re sophisticated professionals or middle-school kids, just have to provide the concepts and the computational thinking, and then the language takes over and automates the details of actually getting things done.
In the past, there always had to be separate systems for kids and professionals to use. But thanks to all this automation, they’ve converged. It’s happened before, in other fields. For example, in video editing. Where there used to be simple systems for amateurs and complicated systems for professionals—but now everyone, from kids to makers of the world’s most expensive movies, uses the very same systems.
It’s probably more difficult to achieve this in computational thinking and programming—but that’s what the past thirty years of work on the Wolfram Language has, I think, now definitively achieved.
In many standard curriculum subjects, kids in school only get to do pale shadows of what professionals do. But when it comes to computational thinking, they’ve now got the same tools—and it’s now realistic for them to do the same professional-grade kinds of things.
Most of what kids get to do in school has, in a sense, little visible leverage. Kids spend a lot of effort to produce one answer in math or chemistry or whatever. If kids write essays, they have to explicitly write out each word. But with computational thinking and the Wolfram Language, it’s a different story. Once a kid understands how to formulate something computationally, and how to write it to the Wolfram Language, then the language takes over to build what’s potentially a big and sophisticated result.
A student might have some idea about the growth and decay of historical empires, and might figure out how to formulate the idea in terms of time series of geographic areas of historical countries. And as soon as they write this idea in the Wolfram Language, the language takes over, and pretty soon the student has elaborate tables and infographics and whatever—from which they can then draw all sorts of conclusions.
But what do kids learn from writing things in the Wolfram Language? Well, first and foremost, they learn computational thinking. Computational thinking is really a new way of thinking. But it’s got certain similarities in its character to other things kids do. Like math, for example, it forces a certain precision and clarity of thinking. But like writing, it’s fundamentally about communicating ideas. And also like writing, it’s a fundamentally creative activity. Good code in the Wolfram Language, like good writing, is clear and elegant—and can readily be read and understood. But unlike ordinary writing, humans aren’t the only target audience: it’s also for computers, to tell them what to automatically do.
When students do problems in math or chemistry or other subjects, the only way they can typically tell if they’ve got the right answer is for their teacher to tell them, or for them to “look it up in the back of the book”. But it’s a whole different story with Wolfram Language code. Because kids themselves can tell if they’re on the right track. The code was supposed to make a honeycomb-like array. Well, did it?
The whole process of creating code is a little different from anything else kids normally do. There’s formulating the code, and then there’s debugging it. Debugging is a very interesting intellectual exercise. The mechanics of it are vastly easier in the Wolfram Language than they’ve ever been before—because the Wolfram Language is symbolic, so any fragment of code can always be run on its own, and separately studied.
But debugging is ultimately about understanding, and problem solving. It’s a very pure form of what comes up in a great many things in life. But what’s really nice about it—particularly in the Wolfram Language—is the instant feedback. You changed something; did it help? Or do you have to dive in and figure out something else?
Part of debugging is just about getting a piece of code to produce something. But the other part is understanding if it produces the right thing. Is that really a sensible social network for the Shakespeare play? Why are there lots of characters who don’t seem to connect to anyone else? Let’s understand how we defined “connectivity”. Does it really make sense? Is there a better definition?
This is the kind of thing computational thinking is about. It’s not so much about programming: it’s about what should be programmed; it’s about the overall problem of formulating things so they can be put into computational form. And now—with today’s Wolfram Language—we have an environment for taking what’s been formulated, and actually turning it into something real.
Most subjects that are taught in school are somewhat tightly constrained. Questions can be asked, but they’re more like typical “tech support”: help me to understand this existing feature. They’re not like “let’s talk about something new”. A few times I’ve done “ask me anything” sessions about science with kids. It’s an interesting experience. There’ll be a question where, yes, it can easily be answered from college-level physics. Then another question that might require graduate-level knowledge. And then—whoosh—there’ll be an obvious-sounding question which I know simply hasn’t been answered, even by the latest leading-edge research.
Or maybe one where, yes, I know the answer, but only because just last month I happened to talk to the world expert who recently figured out. Before I tried these kinds of “ask me anything” sessions I didn’t really appreciate how hard it can be when kids ask “free-range” questions. But now I understand why unless one has teachers with broad research-level knowledge there’s little choice but to make traditional school subjects much more tightly constrained.
But there’s something new that’s possible using the Wolfram Language as a tool. Because with the Wolfram Language a teacher doesn’t have to know the whole answer to a question: they just have to be able to formulate the question in a computational way, so the Wolfram Language can compute the answer. Yes, there’s skill required on the part of the teacher to be able to write in the Wolfram Language. But it’s really fun—and educational—for student and teacher together to be getting the answers to questions.
I’ve often done what I call “live experiments”. I take some topic—either suggested by the audience, or that I thought of just before I start—and then I explore that topic live with the Wolfram Language, and see what I can discover about it. It’s gotten a lot easier over the years, as the capabilities and level of automation in the Wolfram Language have increased. I usually open our Wolfram Summer School by doing a live experiment.
And I’ll make the claim that over the course of an hour or so, we’ll build up a notebook where we’ve discovered something new and interesting enough that it could be the seed for an academic paper or the like. It can be quite nerve-wracking for me. But in almost all cases it works out extremely well. And I think it’s an educational and empowering thing to watch. Because most people don’t realize that it’s even faintly possible to go from zero to a publishable discovery in an hour. But that’s what the modern Wolfram Language makes possible. And while it obviously helps that I personally have a lifetime of experience in computational thinking and discovering things, it’s surprisingly easy for anyone with decent knowledge of computational thinking and the Wolfram Language to do a very compelling live experiment.
When I was a kid I was never a fan of exercises in textbooks. I always took the point of view that it wasn’t very exciting to do the same thing lots of people had already done. And so I always tried to think of different questions that I could explore, and where I could potentially see things that nobody had seen before. Well, in modern times with the Wolfram Language, doing things that have never been done before has become vastly easier. Not every kid has the same motivation structure as I had.
But for many people there’s extra satisfaction in being able to make something that’s really their own creation—and not just a re-run of what’s been made before. And at a practical level, it’s great that with the Wolfram Cloud it’s easy to share what’s made—and for example to create one’s own active website or app, that one can show to one’s class, one’s friends, or the world.
So where are there discoveries that can be made by kids? Everywhere! Even in a technical, well-developed area like math, there’s endless experimental mathematics to be done, where discoveries can be made. In the sciences, there’s a small additional hurdle, because one’s typically got to deal with actual data. Of course, there’s lots of data built right into the Wolfram Language. And it’s easier than ever to get more data. Perhaps one just uses a camera or a microphone, or, more elaborately, one gets sensors connected through Raspberry Pi or Arduino, or whatever.
So what about the humanities? Well, here again one needs data. But again there’s lots of it that’s built right into the Wolfram Language (images of famous artworks, texts of famous books, information on historical countries, and so on and so on). And in today’s world, it’s become extremely easy to find more data on the web—and to import it into the Wolfram Language. Sometimes there’s some data curation involved (which itself is interesting and educational), but it’s amazing in modern times how easy it’s become to find, for example, even obscure documents from centuries ago on the web. (And, yes, that’s one of the things that’s really helped my own hobby of studying history.)
Computational thinking is an area that really lends itself to project-based learning. Every year forour summer programs, I come up with hundreds of ideas for projects that are accessible to kids. And with a little help, the kids themselves come up with even more. For our summer programs, we have kids work on projects on their own, but it’s easy for kids to collaborate on these projects too. We typically have a definite end point for projects: create a Demonstration, or a web app, and write a description, perhaps to post on the Wolfram Community. (Particularly with Demonstrations for ourWolfram Demonstrations Project, the actual process of review and publication tends to be educational too.)
Of course, even when a particular project has been “done before”, it’ll usually be different if it’s done again. At the very simplest level, writing code is a creative process and different people will write it differently. And if there are visualizations or user interfaces as part of the project, each person can creatively invent new ways to do these.
But, OK, all this creative stuff is well and good. But in practice a lot of education has to be done in more of a production-line mode, with large numbers of students in some sense always doing the same thing. And even with this constraint, there’s something good about computational thinking, and coding in the Wolfram Language. One of the convenient features of math is that when people do exercises, they get definite answers, which are easy to check (well, at least up to issues of equivalence of algebraic expressions, which basically needs our whole math technology stack to get right).
When people write essays, there’s basically no choice but to have actual humans read them (yes, one can determine some things with natural language processing and machine learning, but the real point of essays is to communicate with humans, and ultimately to tell if that’s working you really need humans in the loop).
Well, when one writes a piece of code, it’s a creative act, like writing an essay. But now one’s making something that’s set up to be communicated to a computer. And so it makes perfect sense to have a computer read it and assess it. It’s still not a trivial task, though. Because, for example, one wants to check that the student didn’t in effect just put the final answer right into the code they wrote—and that the code really did express, preferably with clarity, a computational idea. It gets pretty high tech, but by using the symbolic character of the Wolfram Language, plus some automated theorem proving and machine learning, it seems to be possible to do very well on this in practice. And that’s for example what’s allowed us to put automatically graded versions of the exercises from myElementary Introduction book on the web.
At one level one can assess what’s going on by looking at the final code students write. Even though there may be an infinite number of different possible programs, one can assess which ones are correct, and even which ones satisfy particular efficiency or elegance criteria. But there’s much further one can go. Because unlike an area like math where students tend to do their thinking on scratch paper, in coding each step in the process of writing a program tends to be done on the computer, with every keystroke able to be captured. I myself have long been an enthusiast ofpersonal analytics, and occasionally I’ve done at least a little analysis on the process by which I write and debug programs.
But there’s a great opportunity in education for this, first in producing elaborate educational analytics (for which the Wolfram Language and Wolfram Cloud are a perfect fit), and then for creating deep ways of adapting to the actual behavior and learning process of each individual student.
Ultimately what we presumably want is an accurate computational model of every student. And with the current machine learning technology that we have in the Wolfram Language I think we’re beginning to have what’s needed to build it.
Given this model what we’d then presumably do is in effect to run lots of simulations of what would happen if the student were told this or that, trying to determine what the optimal thing to explain, or optimal exercise to give, would be at any given time.
In helping with an area like basic math, this kind of personalization is fairly easy to do with simple heuristics. When it comes to helping with coding and computational thinking, the problem is considerably more complicated. But it’s a place where, with good computational thinking, and sophisticated computation inside the system, I think it’ll be possible to do something really good.
I might mention that there’s always a question of what one should assess to find out if someone has really understood a particular thing. With a good computational model of every student, one could have a very sophisticated answer to this. But somewhere one’s still going to have to invent types of exercises or tests to give (well, assuming that one doesn’t just go for the arguably much better scheme of just assessing whole projects).
One fundamental type of exercise—of which my Elementary Introduction is full—is of the form “write a piece of code to do X”. But there are others too. One is “simplify this piece of code”, or “find an input where this function will fail”. Of course, there are exercises like “what will this piece of code do?”. But in some sense exercises like that seem silly: after all, one can just run the code to find out.
Now, I have to say I think it’s useful for people to do a bit of “acting like a computer”. It’s helpful in understanding what computation is, and how the process of computation works. But it’s not something to do a lot of. The real focus, I think, should be on educating people about what they themselves actually need to do.
There is technology and automation in the world, and there’ll be more of it over time. There’s no point in teaching people to do a computer’s job; one should teach them to do what only they can do, working with the computer as a tool and partner, in the best possible way.
(I’ve heard arguments about teaching kids how to do arithmetic without calculators that go along the lines of “what if you were on a desert island without a calculator?”. And I can hear it now having someone make the same argument about teaching kids how to work out what programs do by hand. But, err, if you’re on a desert island without a computer, why exactly are you writing code? [Of course, when code literacy becomes more universal, it might be a different story, because humans on a desert island might be writing code to read themselves...])
OK, so what are the important things to teach? Computational thinking is really about thinking. It’s about formulating ideas in a structured way, that, conveniently enough, can in the modern world be communicated to a computer, which can then do interesting things.
There are facts and ideas to know. Some of them are about the abstract process of computation. But some of them are about how things in the world get made systematic. How is color represented? How are points on the Earth specified? How does one represent the glyphs of different human languages? And so on. We made a poster a few years ago of the history of the systematic representation of data. Just the content of that poster would make an interesting course.
But, OK, so if one knows something about how to represent things, and about the processes of computation, what should one learn how to figure out? The fundamental goal is to get to the point where one’s able to take something one wants to know or do, and be able to cast it into computational form.
Often that’s about “inventing an algorithm”, or “inventing a heuristic”. What’s a good way to compare the growth of the Roman Empire with the spread of the Mongols? What’s the right thing to compute? The right thing to display? How can one tell if there are really more craters near the poles of the Moon? What’s a good way to identify a crater from an image anyway?
It’s the analog of things like this that are at the core of making progress in basically every “computational X” field. And it’s people who learn to be good at these kinds of things who will be the most successful in these fields. Around our company, many of these “invent an algorithm; invent a heuristic” kinds of problems are solved every day—and that’s a large part of what’s gone into building up the Wolfram Language, and Wolfram|Alpha, all these years.
Yes, once the algorithm or the heuristic is invented, it’s up to the computer to execute it. But inventing it is typically first and foremost about understanding what’s wanted in a clear and structured enough way that it can be made computational. With effort, one can invent disembodied exercises that are as abstract as possible. But what’s much more common—and useful—is to have questions that connect to the outside world.
Even a question like “Given a bunch of x,y pairs, what’s a good algorithm for deciding if one should plot them as separate points, or with a line joining them?” is really a question that depends on thinking about the way the world is. And from an educational point of view, what’s really nice about questions of computational thinking is that they almost inevitably involve input from other domains of knowledge. They force a certain kind of broad, general thinking, and a certain application of common sense, that is incredibly valuable for so much of what people need to do.
Well, in the Wolfram Language the idea is that one should be able to take ideas as humans formulate them with computational thinking, and convert them as directly as possible into code in the language. In some small cases (and they’ll gradually get a bit bigger) it’s possible to just specify what one wants in English. But normally one’s writing directly in the Wolfram Language. Which means at some level one’s doing coding, otherwise known as programming.
It’s a much higher-level form of programming, though, than most programmers are used to. And that’s precisely why it’s now accessible to a much broader range of people, and why it makes sense to inject it on a large scale into education.
So how does it relate to “traditional” programming education? There are really two types of programming education that have been tried: what one might call the “high-school version” and the “elementary-school version”. These days the high-school version is mostly about C++ and Java. The elementary-school version is mostly about derivatives of Logo like Scratch. I’ve been shocked, though, that even among technically-oriented kids educated at sophisticated schools in the US, it’s still surprisingly rare to find ones who’ve learned any serious amount of programming in school.
But when they do learn about “programming”, say in high school, what do they actually learn? There’s usually a lot of syntactic detail, but the top concepts tend to be conditionals, loops and variables. As someone who’s spent most of his life thinking about computation, this is really disappointing. Yes, these concepts are certainly part of low-level computer languages. But they’re not central to what we now broadly understand as computation—and in computational thinking in general they’re at best side shows.
What is important? In practice, probably the single most important concept is just that everything (text, images, networks, user interfaces, whatever) can be represented in computational form. Ideas like functions and lists are also important. And if one’s being intellectual, the notion of universal computation (which is what makes software possible) is important too.
But the problem is that what’s being taught now is not only not general computational thinking, it’s not even general programming. Conditionals, loops and variables were central to the very first practical computer languages that emerged in the 1960s. Today’s computer languages—like C++ and Java—have much better ways to manage large volumes of code. But their underlying computational structure is remarkably similar to the 1960s languages. And in fact kids—who are typically writing very small amounts of code—end up really just dealing with computing as it was in the 1960s (though perhaps with a mechanisms aimed at large codebases making it more complicated).
The Wolfram Language is really a language of modern times. It wouldn’t have been practical at all in the 1960s: computers just weren’t big and fast enough, and there wasn’t anything like the cloud in which to maintain a large knowledgebase. (As it happens, there were languages like LISP and APL even in the early 1960s that had higher-level ideas reminiscent of the Wolfram Language, but it took decades before those ideas could really be used in practice.)
So what of loops and conditionals and variables? Well, they all exist in the Wolfram Language. They just aren’t front and center concepts. In my Elementary Introduction book, for example, it’s Chapter 38 before I talk about assigning values to variables, and it happens after I’ve discussed deploying sophisticated knowledge-based apps to the web.
To give an example, let’s say one wants to make a table of the first 10 squares. In the Wolfram Language one could do this very simply, with:
But if one’s working in C for example, it’d be roughly:
A non-programmer might ask: “What the heck is all that stuff?” Well, instead of just saying directly what we want, what it’s doing is telling the computer at a low level exactly what it should do. We’re telling it to allocate memory to store the integer value of n. We’re saying to start with n=1, and keep incrementing n until it gets to 10. And then we’re saying in each case to the computer that it should print the square. There’s a lot of detail. (To be fair, in a more modern language like Python or JavaScript, some of this goes away, but in this example we’re still left dealing with an explicit loop and its variable.)
Now, the crucial point is that the loops and conditionals and variables aren’t the real point of the computation; they’re just details of the particular implementation in a low-level language. I’ve heard people say it’s simpler for kids to understand what’s going on when there are explicit loops and conditionals and variables. From my observations this simply isn’t true. Maybe it’s something that’s changed over the years, as people have gotten more exposed to computation and computational ideas in their everyday lives. But as of now, talking about the details of loops and conditionals and variables just seems to make it harder for kids to understand the concepts of computation.
Is it useful to learn about loops and conditionals and variables at some point? Definitely. They’re part of the whole story of computation and computational thinking. They’re just not the most important part, or the first part to learn. Oh, and by the way, if one’s going to start talking about doing computation with images or networks or whatever, concepts like loops really aren’t what one wants at all.
One important feature of the Wolfram Language is that in its effort to cover general computational thinking it integrates a large number of different computational paradigms. There’s functional programming. And procedural programming. And list-based programming. And symbolic programming. And machine learning and example-based programming. And so on. So when people learn the Wolfram Language, they’re immediately getting exposed to a broad spectrum of computational ideas, conveniently all consistently packaged together.
But what happens when someone who’s learned programming in the Wolfram Language wants to do low-level programming in C++ or Java? I’ve seen this a few times, and it’s been quite charming. They seem to have no difficulty at all grasping how to do good programming in these lower-level languages, but they keep on exclaiming about all the quaint things they have to do, and all the things that don’t work. “Oh my gosh, I actually have to allocate memory myself”. “Wow, there’s a limit on the size of an integer”. And so on.
The transition from the Wolfram Language to lower-level languages seems to be easy. The other way around it’s sometimes a little more challenging. And I must say that I often find it easier to teach computational thinking to kids who know nothing about programming: they pick up the concepts very quickly, and they don’t have to unlearn the idea that everything must turn into loops and conditionals and so on.
When I started considering teaching computational thinking and the Wolfram Language to kids, I imagined it would mostly be high-school kids. But particularly when my Introduction book came out, I was surprised to learn that all sorts of 11- and 12-year-olds were going through it. And my current conclusion is that what we’ve got with Wolfram Programming Lab and so on is suitable for kids down to about age 11 or 12.
What about younger kids? Well, in today’s world, all of them are using computers or smartphones, and are getting exposed to all sorts of computational activities. Maybe they’re making and editing videos. Maybe they’re constructing assets for a game. And all of these kinds of activities are good precursors to computational thinking.
Back in the 1960s, a bold experiment was started in the form of Logo. I’m told the original idea was to construct 50 “microworlds” where kids could experiment with computers. The very first one involved a “turtle” moving around on the screen—and over the course of a half-century this evolved into things like Scratch (which has an orange cat rather than a turtle). Unfortunately, however, the other 49 microworlds never got built. And while the turtle (or cat) is quite cute (and an impressive idea for the 1960s), it seems disappointingly narrow from the point of view of today’s understanding and experience of computation.
Still, lots of kids are exposed to things like Scratch in elementary school—even if sometimes only for a single “hour of code” in a year. In past years, there was clear value in having younger kids get the idea that they could make a computer do what they want at all. But the proliferation of other ways young kids use computation and computational ideas has made this much less significant. And yes, teaching loops and conditionals to elementary-school kids does seem a bit bizarre in modern times.
I strongly suspect that there are some much better ways to teach ideas of computational thinking at young ages—making use of all the technology and automation we have now. One feature of systems like Scratch is that their programs are assembled visually out of brick-like blocks, rather than having to be typed. Usually in practice the programs are quite linear in their structure. But the blocks do two things. First, they avoid the need for any explicit syntax (instead it’s just “does the block fit or not?”). And second, by having a stack of possible blocks on the side of the screen, they immediately document what’s possible.
And perhaps even more important: this whole setup forces one to have only a small collection of possible blocks, in effect a microworld. In the full Wolfram Language, there are over 5000 built-in functions, and just turning them all into blocks would be overwhelming and unhelpful. But the point is to select out of all these possible functions several (50?) microworlds, each involving only a small set of functions, but each chosen so that rich and interesting things can be done with them.
With our current technology, those microworlds can readily involve image computation, or natural language understanding, or machine learning—and, most importantly, can immediately relate to the real world. And I strongly suspect that by including some of these far-past-the-1960s things, we’ll be able to expose young kids much more directly and successfully to ideas about computational thinking that they’ll be able to take with them when they come to learn more later.
I’m trying to do my part, for example, by writing my Elementary Introduction to the Wolfram Language, releasing Wolfram Programming Lab, and creating the free Wolfram Open Cloud. But these are just first steps. There need to be lots of books and courses aimed at different populations. There need to be online and offline communities and activities defined. There need to be ways to deliver what’s now possible to students. And there need to be ways to teach teachers how to help.
We’ve got quite a few basic things in the works. A packaged course based on the Elementary Introduction. A Wolfram Challenges website with coding and computational thinking challenges. A more structured mentorship program for individual students doing projects. A franchisable version of our Wolfram Summer Camp. And more. Some of these are part of Wolfram Research; some come from the Wolfram Foundation. We’re considering a broader non-profit initiative to support delivering computational thinking education. And we’ve even thought about creating a whole school that’s centered around computational thinking—not least to show at least one model of how it can be done.
But beyond anything we’re doing, what I’m most excited about is that other people, and other organizations, are starting to take things forward, too. There are in-school programs, after-school programs, summer programs. There are the beginnings of very large-scale programs across countries.
Our own company and foundation are fairly small. To be able to educate the world about computational thinking, many other people and organizations need to be involved. Thanks to three decades of work we are at the point where have the technology. But now we have to actually get it delivered to kids all over the world in the right way.
Computational thinking is something that I think can be successfully taught to a very wide range of people, regardless of their economic resources. And because it’s so new, countries or regions with more sophisticated educational setups, or greater technological prowess, don’t really have any great advantage over anyone else in doing it.
Eventually, much of the world’s population will be able to do computational thinking and be able to communicate with computers using code—just as they can now read and write. But today we’re just at the beginning of making this happen. I’m pleased to be able to contribute technology and a little more to this. I look forward to seeing what I hope will be rapid progress on this in the next year or so, and in the years to come.
About the Author:
Stephen Wolfram is
- Founder & CEO of Wolfram Research
- Creator of Mathematica, Wolfram|Alpha
- & the Wolfram Language
- Author of A New Kind of Science